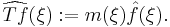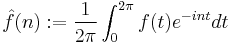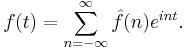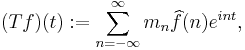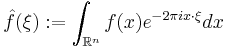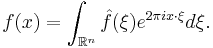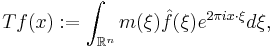Multiplier (Fourier analysis)
In Fourier analysis, a multiplier operator is a type of linear operator, or transformation of functions. These operators act on a function by altering its Fourier transform. Specifically they multiply the Fourier transform of a function by a specified function known as the multiplier or symbol. Occasionally, the term "multiplier operator" itself is shortened simply to "multiplier" (Duoandikoetxea 2001, 3.5). In simple terms, the multiplier reshapes the frequencies involved in any function. This class of operators turns out to be broad: general theory shows that a translation-invariant operator on a group which obeys some (very mild) regularity conditions can be expressed as a multiplier operator, and conversely. Many familiar operators, such as translations and differentiation, are multiplier operators, although there are many more complicated examples such as the Hilbert transform.
In signal processing, a multiplier operator is called a "filter", and the multiplier is the filter's frequency response (or transfer function).
In the wider context, multiplier operators are special cases of spectral multiplier operators, which arise from the functional calculus of an operator (or family of commuting operators). They are also special cases of pseudo-differential operators, and more generally Fourier integral operators. There are natural questions in this field that are still open, such as characterizing the 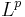 bounded multiplier operators (see below). In this context, multipliers are unrelated to Lagrange multipliers, except for the fact that they both involve the multiplication operation.
bounded multiplier operators (see below). In this context, multipliers are unrelated to Lagrange multipliers, except for the fact that they both involve the multiplication operation.
For the necessary background on the Fourier transform, see that page. Additional important background may be found on the pages operator norm and Lp space.
Contents |
Examples
In the setting of periodic functions defined on the unit circle, the Fourier transform of a function is simply the sequence of its Fourier coefficients. To see that differentiation can be realized as multiplier, consider the Fourier series for the derivative of a periodic function ƒ(t). After using integration by parts in the definition of the Fourier coefficient we have that
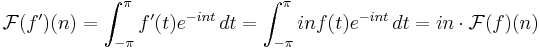 .
.
So, formally, it follows that the Fourier series for the derivative is simply in multiplied by the Fourier series for ƒ. This is the same as saying that differentiation is a multiplier operator with multiplier in.
An example of a multiplier operator acting on functions on the real line is the Hilbert transform. It can be shown that the Hilbert transform is a multiplier operator whose multiplier is given by the m(ξ) = −i sgn(ξ), where sgn is the signum function.
Finally another important example of a multiplier is the characteristic function of the unit ball in ℝn which arises in the study of "partial sums" for the Fourier transform (see Convergence of Fourier series).
Definition
Multiplier operators can be defined on any group G for which the Fourier transform is also defined (in particular, on any locally compact amenable abelian group). The general definition is as follows. If 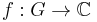 is a sufficiently regular function, let
is a sufficiently regular function, let 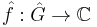 denote its Fourier transform (where
denote its Fourier transform (where 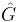 is the Pontryagin dual of G). Let
is the Pontryagin dual of G). Let 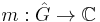 denote another function, which we shall call the multiplier. Then the multiplier operator
denote another function, which we shall call the multiplier. Then the multiplier operator 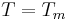 associated to this symbol m is defined via the formula
associated to this symbol m is defined via the formula
In other words, the Fourier transform of 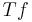 at a frequency
at a frequency 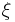 is given by the Fourier transform of
is given by the Fourier transform of  at that frequency, multiplied by the value of the multiplier at that frequency. This explains the terminology "multiplier".
at that frequency, multiplied by the value of the multiplier at that frequency. This explains the terminology "multiplier".
Note that the above definition only defines 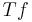 implicitly; in order to recover
implicitly; in order to recover 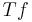 explicitly one needs to invert the Fourier transform. This can be easily done if both f and m are sufficiently smooth and integrable. One of the major problems in the subject is to determine, for any specified multiplier m, whether the corresponding Fourier multiplier operator continues to be well-defined when f has very low regularity, for instance if it is only assumed to lie in an
explicitly one needs to invert the Fourier transform. This can be easily done if both f and m are sufficiently smooth and integrable. One of the major problems in the subject is to determine, for any specified multiplier m, whether the corresponding Fourier multiplier operator continues to be well-defined when f has very low regularity, for instance if it is only assumed to lie in an 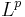 space. See the discussion on the "boundedness problem" below. As a bare minimum, one usually requires the multiplier m to be bounded and measurable; this is sufficient to establish boundedness on
space. See the discussion on the "boundedness problem" below. As a bare minimum, one usually requires the multiplier m to be bounded and measurable; this is sufficient to establish boundedness on 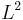 but is in general not strong enough to give boundedness on other spaces.
but is in general not strong enough to give boundedness on other spaces.
One can view the multiplier operator T as the composition of three operators, namely the Fourier transform, the operation of pointwise multiplication by m, and then the inverse Fourier transform. Equivalently, T is the conjugation of the pointwise multiplication operator by the Fourier transform. Thus one can think of multiplier operators as operators which are diagonalized by the Fourier transform.
Multiplier operators on common groups
We now specialize the above general definition to specific groups G. First consider the unit circle 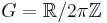 ; functions on G can thus be thought of as
; functions on G can thus be thought of as 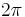 -periodic functions on the real line. In this group, the Pontryagin dual is the group of integers,
-periodic functions on the real line. In this group, the Pontryagin dual is the group of integers, 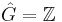 . The Fourier transform (for sufficiently regular functions f) is given by
. The Fourier transform (for sufficiently regular functions f) is given by
and the inverse Fourier transform is given by
A multiplier in this setting is simply a sequence 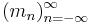 of numbers, and the operator
of numbers, and the operator 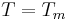 associated to this multiplier is then given by the formula
associated to this multiplier is then given by the formula
at least for sufficiently well-behaved choices of the multiplier 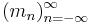 and the function f.
and the function f.
Now let G be a Euclidean space 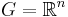 . Here the dual group is also Euclidean,
. Here the dual group is also Euclidean, 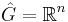 , and the Fourier and inverse Fourier transforms are given by the formulae
, and the Fourier and inverse Fourier transforms are given by the formulae
A multiplier in this setting is a function 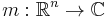 , and the associated multiplier operator
, and the associated multiplier operator 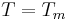 is defined by
is defined by
again assuming sufficiently strong regularity and boundedness assumptions on the multiplier and function.
In the sense of distributions, there is no difference between multiplier operators and convolution operators; every multiplier T can also be expressed in the form 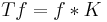 for some distribution K, known as the convolution kernel of T. In this view, translation by an amount x0 is convolution with a Dirac delta function δ(· − x0), differentiation is convolution with δ'. Further examples are given in the table below.
for some distribution K, known as the convolution kernel of T. In this view, translation by an amount x0 is convolution with a Dirac delta function δ(· − x0), differentiation is convolution with δ'. Further examples are given in the table below.
Diagrams
Further Examples
The following table shows some common examples of multiplier operators on the unit circle 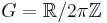 .
.
| Name | Multiplier  |
Operator 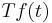 |
Kernel 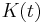 |
|---|---|---|---|
| Identity operator | 1 | f(t) | Dirac delta function 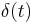 |
| Multiplication by a constant c | c | cf(t) | 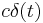 |
| Translation by s | 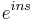 |
f(t − s) | 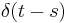 |
| Differentiation | in | f '(t) | 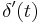 |
| k-fold differentiation | 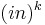 |
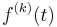 |
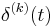 |
| Constant coefficient differential operator | 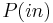 |
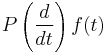 |
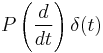 |
Fractional derivative of order  |
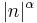 |
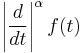 |
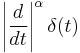 |
| Mean value | 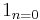 |
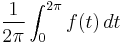 |
1 |
| Mean-free component | 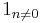 |
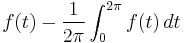 |
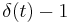 |
| Integration (of mean-free component) | 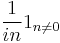 |
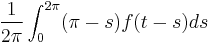 |
Sawtooth function 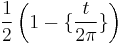 |
| Periodic Hilbert transform H | 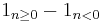 |
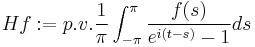 |
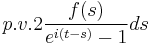 |
Dirichlet summation 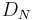 |
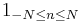 |
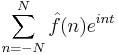 |
Dirichlet kernel 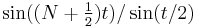 |
Fejér summation  |
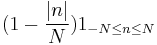 |
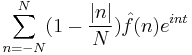 |
Fejér kernel 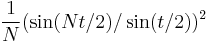 |
| General multiplier |  |
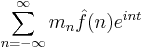 |
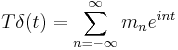 |
| General convolution operator | 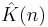 |
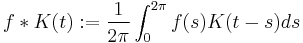 |
 |
The following table shows some common examples of multiplier operators on Euclidean space 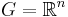 .
.
| Name | Multiplier 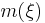 |
Operator 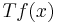 |
Kernel 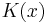 |
|---|---|---|---|
| Identity operator | 1 | f(x) | 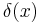 |
| Multiplication by a constant c | c | cf(x) | 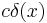 |
| Translation by y | 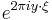 |
f(x − y) | 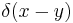 |
Derivative 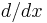 (one dimension only) (one dimension only) |
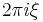 |
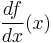 |
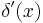 |
Partial derivative 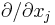 |
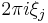 |
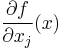 |
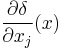 |
Laplacian  |
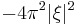 |
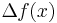 |
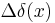 |
Constant coefficient differential operator 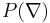 |
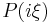 |
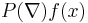 |
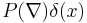 |
Fractional derivative of order  |
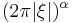 |
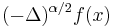 |
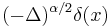 |
Riesz potential of order  |
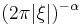 |
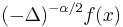 |
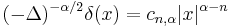 |
Bessel potential of order  |
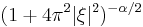 |
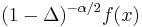 |
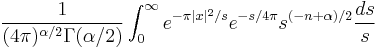 |
Heat flow operator 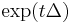 |
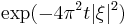 |
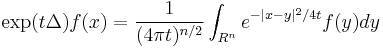 |
Heat kernel 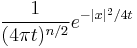 |
Schrödinger equation evolution operator 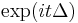 |
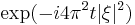 |
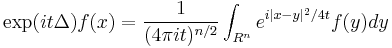 |
Schrödinger kernel 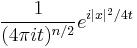 |
| Hilbert transform H (one dimension only) | 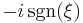 |
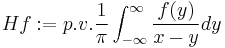 |
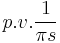 |
| Riesz transforms Rj | 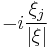 |
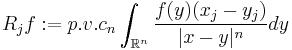 |
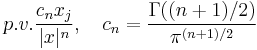 |
Partial Fourier integral 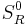 (one dimension only) (one dimension only) |
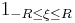 |
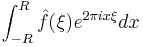 |
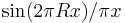 |
Disk multiplier 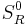 |
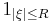 |
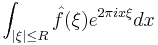 |
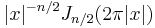 (J is a Bessel function) (J is a Bessel function) |
Bochner–Riesz operators 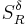 |
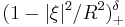 |
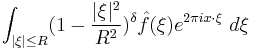 |
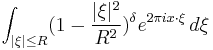 |
| General multiplier | 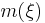 |
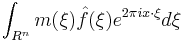 |
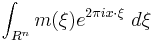 |
| General convolution operator | 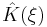 |
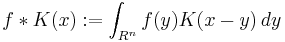 |
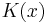 |
General considerations
The map 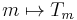 is a homomorphism of C*-algebras. This follows because the sum of two multiplier operators
is a homomorphism of C*-algebras. This follows because the sum of two multiplier operators 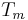 and
and 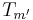 is a multiplier operators with multiplier
is a multiplier operators with multiplier 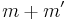 , the composition of these two multiplier operators is a multiplier operator with multiplier
, the composition of these two multiplier operators is a multiplier operator with multiplier 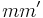 , and the adjoint of a multiplier operator
, and the adjoint of a multiplier operator 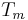 is another multiplier operator with multiplier
is another multiplier operator with multiplier 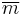 .
.
In particular, we see that any two multiplier operators commute with each other. It is known that multiplier operators are translation-invariant. Conversely, one can show that any translation-invariant linear operator which is bounded on 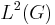 is a multiplier operator.
is a multiplier operator.
The Lp boundedness problem
The 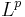 boundedness problem (for any particular p) for a given group G is, stated simply, to identify the multipliers
boundedness problem (for any particular p) for a given group G is, stated simply, to identify the multipliers  such that the corresponding multiplier operator is bounded from
such that the corresponding multiplier operator is bounded from 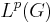 to
to 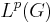 . Such multipliers are usually simply referred to as "
. Such multipliers are usually simply referred to as "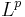 multipliers". Note that as multiplier operators are always linear, such operators are bounded if and only if they are continuous. This problem is considered to be extremely difficult in general, but many special cases can be treated. The problem depends greatly on p, although there is a duality relationship: if
multipliers". Note that as multiplier operators are always linear, such operators are bounded if and only if they are continuous. This problem is considered to be extremely difficult in general, but many special cases can be treated. The problem depends greatly on p, although there is a duality relationship: if 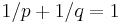 and
and 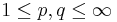 , then a multiplier operator is bounded on
, then a multiplier operator is bounded on 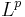 if and only if it is bounded on
if and only if it is bounded on 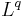 .
.
The Riesz-Thorin theorem shows that if a multiplier operator is bounded on two different 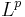 spaces, then it is also bounded on all intermediate spaces. Hence we get that the space of multipliers is smallest for
spaces, then it is also bounded on all intermediate spaces. Hence we get that the space of multipliers is smallest for 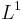 and L∞ and grows as one approaches
and L∞ and grows as one approaches 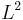 , which has the largest multiplier space.
, which has the largest multiplier space.
Boundedness on L2
This is the easiest case. Parseval's theorem allows to solve this problem completely and obtain that a function m is an 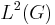 multiplier if and only if it is bounded and measurable.
multiplier if and only if it is bounded and measurable.
Boundedness on L1 or L∞
This case is more complicated than the Hilbertian (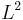 ) case, but is fully resolved. The following is true:
) case, but is fully resolved. The following is true:
Theorem: In the euclidean space ℝn, a function 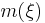 is an
is an 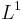 multiplier (equivalently an
multiplier (equivalently an 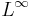 multiplier) if and only if there exists a finite Borel measure μ such that
multiplier) if and only if there exists a finite Borel measure μ such that  is the Fourier transform of μ.
is the Fourier transform of μ.
(The "if" part is a simple calculation. The "only if" part here is more complicated.)
Boundedness on Lp for 1 < p < ∞
In this general case, necessary and sufficient conditions for boundedness have not been established, even for Euclidean space or the unit circle. However, several necessary conditions and several sufficient conditions are known. For instance it is known that in order for a multiplier operator to be bounded on even a single 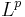 space, the multiplier must be bounded and measurable (this follows from the characterisation of
space, the multiplier must be bounded and measurable (this follows from the characterisation of 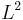 multipliers above and the inclusion property). However, this is not sufficient except when
multipliers above and the inclusion property). However, this is not sufficient except when 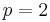 .
.
Results that give sufficient conditions for boundedness are known as multiplier theorems. Two such results are given below.
Marcinkiewicz multiplier theorem
Let 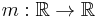 be a bounded function that is continuously differentiable in every set of the form
be a bounded function that is continuously differentiable in every set of the form 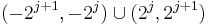 for
for 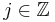 and has derivative such that
and has derivative such that
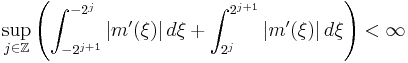 .
.
Then m is an 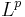 multiplier for all
multiplier for all 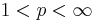 .
.
Mikhlin multiplier theorem
Let  be a bounded function on ℝn which is smooth except possibly at the origin, and such that the function
be a bounded function on ℝn which is smooth except possibly at the origin, and such that the function 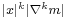 is bounded for all integers
is bounded for all integers 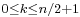 : then m is an
: then m is an 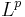 multiplier for all
multiplier for all 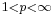 .
.
This is a special case of the Hörmander-Mikhlin multiplier theorem.
The proof of these two theorems are fairly tricky, involving techniques from Calderón–Zygmund theory and the Marcinkiewicz interpolation theorem: for the original proof, see Mikhlin (1956) or Mikhlin (1965, pp. 225–240).
Examples
Translations are bounded operators on any 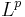 . Differentiation is not bounded on any
. Differentiation is not bounded on any 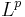 . The Hilbert transform is bounded only for p strictly between 1 and ∞. The fact that it is unbounded on L∞ is easy, since it is well known that the Hilbert transform of a step function is unbounded. Duality gives the same for p = 1. However, both the Marcinkiewicz and Mikhlin multiplier theorems show that the Hilbert transform is bounded in
. The Hilbert transform is bounded only for p strictly between 1 and ∞. The fact that it is unbounded on L∞ is easy, since it is well known that the Hilbert transform of a step function is unbounded. Duality gives the same for p = 1. However, both the Marcinkiewicz and Mikhlin multiplier theorems show that the Hilbert transform is bounded in 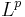 for all
for all 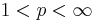 .
.
Another interesting case on the unit circle is when the sequence 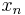 is constant on the intervals
is constant on the intervals ![[2^n,2^{n%2B1}-1]](/2012-wikipedia_en_all_nopic_01_2012/I/d540c76c93121af6099120315948eba5.png) and
and ![[-2^{n%2B1}%2B1,-2^n]](/2012-wikipedia_en_all_nopic_01_2012/I/a850a2597cf1c5622c1702baa0780b1c.png) . From the Marcinkiewicz multiplier theorem (adapted to the context of the unit circle) we see that any such sequence (bounded, of course) is a multiplier for every 1 < p < ∞.
. From the Marcinkiewicz multiplier theorem (adapted to the context of the unit circle) we see that any such sequence (bounded, of course) is a multiplier for every 1 < p < ∞.
In one dimension, the disk multiplier operator 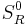 is bounded on
is bounded on 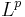 for every
for every 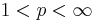 . However, in 1972, Charles Fefferman showed the surprising result that in two and higher dimensions the disk multiplier operator
. However, in 1972, Charles Fefferman showed the surprising result that in two and higher dimensions the disk multiplier operator 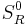 is unbounded on
is unbounded on 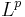 for every
for every 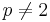 . The corresponding problem for Bochner–Riesz multipliers is only partially solved; see also Bochner–Riesz operator and Bochner–Riesz conjecture.
. The corresponding problem for Bochner–Riesz multipliers is only partially solved; see also Bochner–Riesz operator and Bochner–Riesz conjecture.
A final result concerns a random  :
:
Theorem: Let 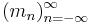 be a symbol consisting of independent variables uniform on [0,1]. Then almost surely the multiplier operator corresponding to this symbol is bounded only
be a symbol consisting of independent variables uniform on [0,1]. Then almost surely the multiplier operator corresponding to this symbol is bounded only 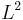 .
.
See also
References
- Duoandikoetxea, Javier (2001), Fourier Analysis, American Mathematical Society, ISBN 0-8218-2172-5
- Loukas Grafakos (2008) Classical Fourier Analysis (Second Edition). Springer, ISBN 9780387094311.
- Yitzhak Katznelson (2004) An Introduction to Harmonic Analysis. Cambridge University Press, ISBN 9780521543590.
- Mikhlin, Solomon G. (1956), "On the multipliers of Fourier integrals", Doklady Akademii Nauk SSSR, n. Ser., 109: 701–703, Zbl 0073.08402 (in Russian).
- Mikhlin, Solomon G. (1965), Multidimensional singular integrals and integral equations, International Series of Monographs in Pure and Applied Mathematics, 83, Oxford-London-Edinburgh-New York-Paris-Frankfurt: Pergamon Press, pp. XII+255, Zbl 0129.07701. A masterpiece in the multidimensional theory of singular integrals and singular integral equations summarizing all the results from the beginning to the year of pubblication, and also sketching the history of the subject.
- Walter Rudin (1962) Fourier Analysis on Groups. Interscience.
- Elias M. Stein (1986) Singular Integrals and Differentiability Properties of Functions. Princeton University Press, ISBN 0697080798.
- Alberto Torchinsky (2004) Real-Variable Methods in Harmonic Analysis. Dover, ISBN 0486435083.